√ダウンロード 階差数列の和の公式 161769-階差数列の和の公式

階差数列とは の階差数列といいます。 つまり、隣同士の差をとったときにあらわれる数列のことです。 （ ）内は第1項から第（n1)項までの和である。これをΣ記号を使って表すと Σの計算の仕方 Σの計算の仕方は後ろに来る文字の次数によって公式がありましたね。 階差数列ではシグマ計算を多用するので、公式を忘れている場合は復習しておきましょう。 和（シグマ \(\bf{\sum}\) ）の計算 \(\displaystyle \sum_{k = 1}^n a = an\) 等差数列の和を求める公式 等差数列の初項からある項までをすべて足し合わせる公式がある。 初項a、末項l、項数nの等差数列の和S n を求める公式は以下。 この公式についても具体的な数列を使いながら証明していきたい。 ＜公式の証明＞

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

階差数列の和の公式

階差数列の和の公式-2,4,8,16,32,64,・・・ のように隣り合う項の比(公比)が等しい数列を等比数列という。初項(一番最初の項)がaで、交比がrである等比数列のn番目の項(an)は次式となる。 an = a・r n1 等比数列の和(Sn)を等比級数といい、次式の公式となる。階差型の数列 タイプ： 教科書範囲 レベル： ★★ 階差数列を用いて一般項を求める方法について解説します． 当サイトではそのような数列を階差型の数列と呼ぶことにし，深く内容を考察，解説し，演習問題まで用意しました． 目次 1： 階差型の数列

高校数学b 和s Nと一般項a Nの関係 受験の月

→4乗の和，べき乗の和の公式 分数の和 例： ∑ k = 1 10 1 k ( k 1 ) = 10 11 \displaystyle\sum_{k=1}^{10}\dfrac{1}{k(k1)}=\dfrac{10}{11} k = 1 ∑ 10 k ( k 1 ) 1 = 11 10階差数列・和と一般項の関係 階差数列 階差数列をbn とするとき an = a1 n∑ 1 k=1 bk (n = 2) 和と一般項の関係 an = Sn −Sn 1 (n = 2) a1 = S1 基本漸化式4 パターン an1 = an p (p は定数) 等差数列 ※p は公差 an1 = ran (r は定数) 等比数列 ※r は公比階差数列の公式を導き方から確認しておきます。 階差数列を表す漸化式の形は決まっているので見抜くのは簡単ですが、 一般項を求める問題でポイントになるのは公式です。 ただ、公式がなくても階差数列の一般項は求めることができます

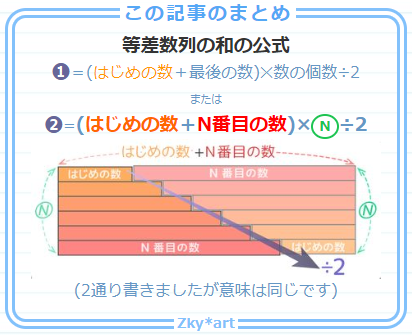
 ＝ (はじめの数 ＋最後の数)✕数字の個数÷2 (例)等差数列 ① 1 ②3 ③5 ⑩19 の和は？ → (1 19)×⑩÷２=100 今の問題は数字が10個しかありませんでしたが、この公式を使って、もっと多くの数字がある数列の合計を出してみましょう！こうしてみると、数列 {a n }の各項は、階差数列を利用して分解できることが分かるだろう。 a 6 =66=4521= (2817)21= (1513)1721= (69)= 等差数列・等比数列を分かりやすく考えるコツ 数列の和を求めるとき、式変形をするたびに毎回数列をすべて書いていたら、スペースがいくらあっても足りません。 そのため、多くの場合は総和記号 Σ （シグマ）を使ってまとめて計算することになり

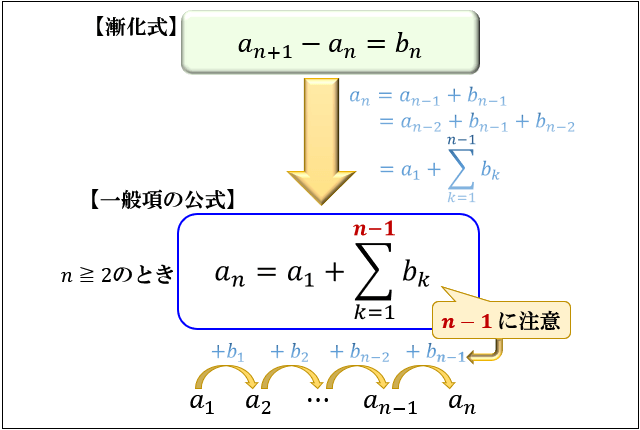
 階差をとったときの等差数列のn1番目 までの和(今の例だと、) を足せば良いことになります。 このとき、和を足すのはn番目まででなく n1番目であることに注意してください。 つまり、まとめるとこうです。 階差数列の 初項がgだとします 2 等比数列とは「同じ数をかけ続ける数列」 21 等比数列の定義を説明！ 22 「初項」「公比」だけを押さえれば一般項は求められる 3 等比数列の和の公式 31 和の公式を証明！ 32 和の公式が出てくる問題で練習しよう 4 大学入試でよく出る応用問題 41 それではここまで学んだ知識を用いて、問題を実際にといてみましょう。 (1) a n = 3 n − 1 となる等差数列の和 S n を求めよ (2) a n = 1, 3, 5, 7, となる数列の a 1 から a 100 までの和を求めよ (3) 等差数列の和が S 100 = 100 を満たす時、 a n を a 1 と n を用いて表せ。

2 5 14 41 122 365の一般項を求めよ が分かりません Clear

等比数列

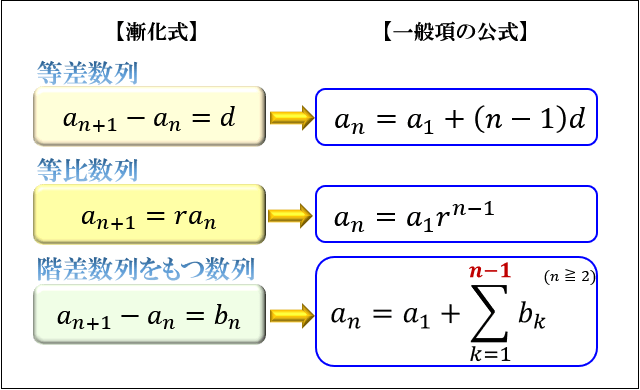
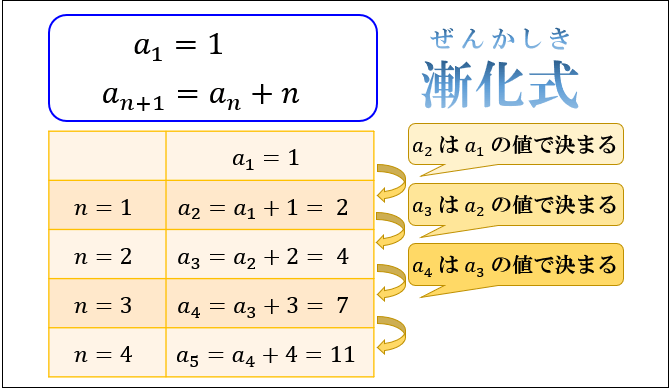
和の公式って何！？中学受験にもでる階差数列！ それでは階差数列の和の公式とはどんな公式でしょうか。 それを示したのが下の図です！ n≧2という場合分けがあるのは数学B ： 数列 公式集 数式の表示がおかしいときは こちら をご覧ください。 印刷用PDFは こちら 絶対憶える 憶える 復習 ですので、等差数列の 番までの和の公式を使って求めることができます。 そして出てきた値に初項を足すと 1＋45＝46となります。 答え46

階差数列

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

数列の各項で下の数列の各項を割った数列 の初項から第6項までを書き込んでみましょ う。（表6,7） 表6表表66表6 表7表表77表7 次に，数列 S n(4) Sn(2) Ç È, S (5) Sn(3) Ç Èの階差数列階差数列階差 階差数列を用いて一般項を求める公式の証明 の階差数列 は の隣り合う2項の差なので、 は2項以上存在していないと を定義することができません。 よって、 (1) である必要があります。 に を代入すると、 上式を全て足すと、 東大塾長の山田です。 このページでは、 数学b数列の「階差数列」について解説します 。 今回は階差数列の一般項の求め方から，漸化式の解き方まで，具体的に問題を解きながら超わかりやすく解説していきます。 ぜひ勉強の参考にしてください！ 1 階差数列とは？

等差数列の一般項と和 おいしい数学

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

 階差数列の和を求める必要がある場合は それぞれ「等差」か「等比」かによって 扱う公式は異なりますね。 一番多いパターンは 数列 {an}の階差数列が {bn}のときに {bn}の一般項が 等差数列や等比数列となるとき {an}の一般項を求める場合だと思います。 このように「差(階差数列)が等差数列になる数列のn番目の数」は「和の公式」を使ってを求めることが出来ます。 等差数列になる「差」を利用 何度も言いますが、 N番目の数を出すときは(N1) です。階差数列 数列 の階差数列が扱いやすい数列の場合。 (19) の各項は、 ～ の和をとることで以下のように得られる。 () 例 の階差数列が で のときの数列 は以下のようになる この数列の一般項は、 (21) 上式は の時も初期条件 を満足する。

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

公式集 数列 おおぞらラボ

4 等差数列の和 前の章で，等差数列の一般項について学習しました。ここでは，その和について考えてみることにしましょう。 ここで，初項 3，公差 2，項数 10 の等差数列 3，5，7，9，11，13，15，17，19，21 を考え，その和を求めてみましょう。 ちなみに、三角数の和を公式化すると、 \(\displaystyle S_n=\frac{ 1 }{ 6 } n ( n 1 ) ( n 2 )\) あれ？どっかで見たような \(\displaystyle \sum_{ k = 1 }^{ n } k^2 =\frac{ 1 }{ 6 } n ( n 1 ) ( 2n 1 )\) \((=1^2 2^2 \cdots n^2)\) ああ！平方数の和の公式とクリソツ。自然数の累乗の和 → 携帯版は別頁 数列の「各項の差」からなる数列を元の数列の階差数列と言います。 例 元の数列よりもその差から作った階差数列の方が簡単な規則性を持っていることが多いので，階差数列で規則性を見つけて，元の数列の一般項を求めることができます。 階差数列の定義 元の数列を { a n }，階差数列を { b n }で表わすとき b n = a n1 a n (n≧1

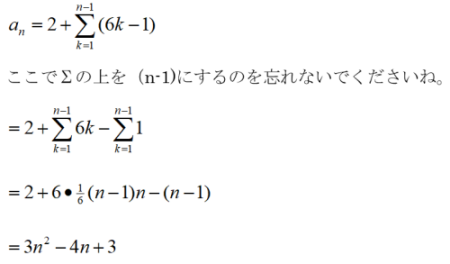
階差数列の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

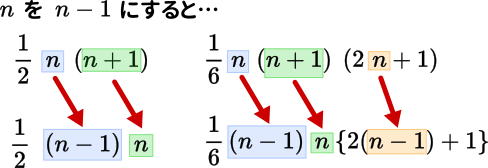
数 ｂ数列 漸化式 階差数列から一般項を求める Mm参考書

・階差数列についての知識を身に付け，意 味を理解している。〔知〕 ・階差数列を利用して，もとの数列の一般 項が求める技能を身に付けている。〔 技〕 観察・ノート 5 時 初項から第n項までの和と一般項の関係を理 解する。また，一般項を求める S n = 1 2 n ( a l) とかけます。 これが等差数列の初項から第 n 項目までの和となるわけですね。 これをみて分かる通りこの公式は初項 a 、一番最後の項（末項と呼びます）と項数 n でかけていることがわかります。 ちなみに末項 l は元の書き方に戻せば aのように、kの関数として表されるものを指す。31のような形式で表された数列 を等差数列、32 のような形式で表された数列を等比数列と呼ぶ。 数列の和は、以下の公式を使って求めることができる。 ∑n k=1 k = 1 2 n(n1) (33) ∑n k=1 k2 = 1 6 n(n1)(2n1) (34) ∑n k=1 rk = r(rn −1) r −1

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

階差数列の一般項 数学b フリー教材開発コミュニティ Ftext

元の数列を｛ａ ｎ ｝，階差数列を｛ｂ ｎ ｝とおくと，｛ｂ ｎ ｝は １，４，９，１６，２５・・・ ｂ ｎ = ［ア］ n≧2のとき， これはn=1のときも成り立つ。階差数列を使って一般項を求める公式 数列\(\{a_n\} \) の階差数列を\(\{b_n\}\) とすると、 \(n≧2\) のとき $$a_n=a_1\displaystyle \sum_{ k = 1 }^{ n1 } b_k$$階差数列の公式中には ∑ i = 1 n − 1 \displaystyle\sum_{i=1}^{n1} i = 1 ∑ n − 1 という表記が含まれており， n ≥ 2 n\geq 2 n ≥ 2 でないと意味を持ちません。そのため， n ≥ 2 n\geq 2 n ≥ 2 と n = 1 n=1 n = 1 の場合を分けて考える必要があります。

Left Anright 1 4 10 22 Descubre Como Resolverlo En Qanda

分数の数列の和 高校数学ｂ Youtube

数列 怜悧玲瓏 高校数学を天空から俯瞰する

等差数列の和の公式と階差数列の公式はおなじでしょうか 問 Yahoo 知恵袋

階差数列 数列の和の問題です F1 数学 箱根駅伝ブログ

A10 Bn Bn Descubre Como Resolverlo En Qanda

高校数学b 階差数列から一般項を求める １ 練習編 映像授業のtry It トライイット

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

3

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

等比数列の一般項と和 おいしい数学

高校数学b 等比数列 A N の一般項 ２ 練習編 映像授業のtry It トライイット

階差数列の和 三角数 父ちゃんが教えたるっ

誤答から学ぼうシリーズ 等差数列 等比数列 型の数列の和 ほのぼの数学頑張ろう

階差数列のちょっとした小手技

数列公式集 Flashcards Quizlet

等差数列の一般項や和の公式をマスターしよう ますますmathが好きになる 魔法の数学ノート

等比数列の和の公式で次の2つを習いました しかしこの2つの使い分けがイマ Yahoo 知恵袋

高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月

高校数学b 階差数列から一般項を求める １ 練習編 映像授業のtry It トライイット

階差数列を利用して数列の一般項を求める問題です Clear

階差数列の和 について 数学b 数列

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

階差数列を用いて一般項を求める方法 思考力を鍛える数学

等差 等比 の和 2次式 等比 の和 おいしい数学

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

階差型の数列 おいしい数学

高校数学b 階差を利用する和 連続整数の積の和 Sk K 1 K 2 受験の月

高校数学b 和s Nと一般項a Nの関係 受験の月

階差数列の考え方 高校数学の知識庫

高校数学b 等差 等比 型 2次式 等比 型の数列の和 受験の月

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

等比数列

階差数列 N 1 のとき成り立たない数列の作り方 怜悧玲瓏 高校数学を天空から俯瞰する

中学受験 差 階差数列 を利用する問題の解き方 無料プリントあり そうちゃ式 受験算数 新1号館

漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

高校数学b 階差を利用する和 根号型 対数型 階乗型 受験の月

数列の基本５ 階差数列の考え方は簡単 階差数列の公式

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

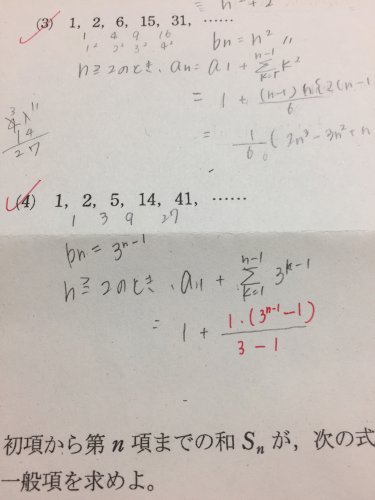
この赤で書いたところはなんの公式ですか 階差数列を利用して次の数 その他 教育 科学 学問 教えて Goo

階差数列の考え方 高校数学の知識庫

例題で学ぶ高校数学 階差数列

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

1

数列と級数 京極一樹の数学塾

階差数列の和 について 数学b 数列

オレンジペンで示したところがわかりません 階差数列というより 数列の和の公式でつまづ Clear

いろいろな数列 3

階差数列の数列の和と一般項 のところで 2 1 2 7 14 Yahoo 知恵袋

階差数列の一般項anを求める問題の途中式を詳しく教えて下さい 式の作り Yahoo 知恵袋

高校数学b 等比数列 A N の和 １ 映像授業のtry It トライイット

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

階差数列なんですが 第n 1項までの和を出すときに 等差数列の和の公式をつかいますよ Clear

1乗和 2乗和 3乗和の公式 導出法から理解しよう

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

なぜ階差数列の一般項は2のn乗になるのか分かりません Clear

数学b 数列 階差数列 和 オンライン無料塾 ターンナップ

階差数列を用いて一般項を求める方法について 高校数学の美しい物語

階差数列を利用して元の数列の一般項を求める問題について ほのぼの数学頑張ろう

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

５月５日 小６算数 Gw特講 ジャングルジムブログ

なんで初項2 公比2の等比数列とわかるのですか Clear

階差数列

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

2

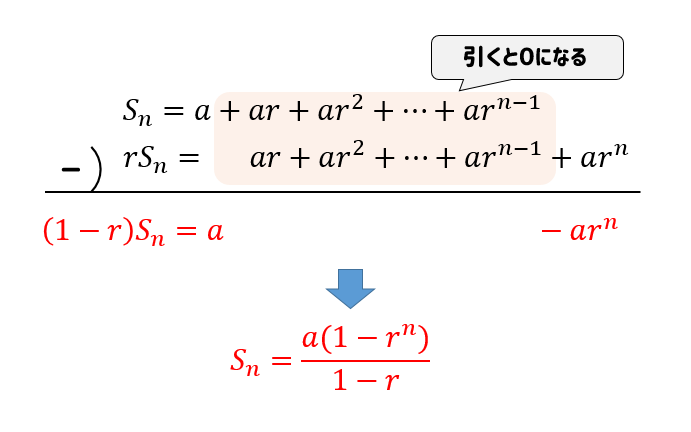
数列の基本２ 等差数列の和の公式 と 等比数列の和の公式

数列の和と階差数列 Taustation

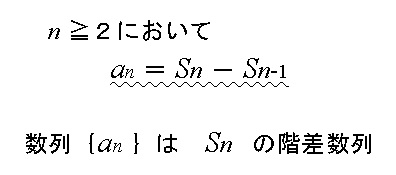
数列 の記事一覧 3 4ページ目

数列 奇数の和 を求める 大人が学び直す数学

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

いろいろな数列の和 N 2のとき と定義する問題としない問題があります 数学 教えて Goo

1

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

Excel エクセルで等比数列の和を計算する方法

数列の教え方 キムチャート 塾で高校生に数学を教える方法

無限等比級数とは 基本からわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

1

数学b 数列 和から一般項を求める オンライン無料塾 ターンナップ

2

無限等比級数とは 基本からわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

階差数列

Incoming Term: 階差数列の和の公式,